The Smarter Balanced Assessment Consortium (SBAC) Mathematics Assessment is a critical component of student evaluation in many states across the country. This comprehensive SBAC Math Practice Test guide provides parents and students with essential information about the math test structure, content, strategies, and sample questions to help maximize performance on the 2025 assessments.
What is the SBAC Math Test? [Essential Overview]
The SBAC Math assessment is meticulously designed to measure students' progress toward Common Core mathematical standards. This isn't about memorization—it's about demonstrating authentic mathematical thinking that translates to real-world applications.
What makes this assessment particularly powerful is its adaptive format. As students progress through the test, the difficulty adjusts based on their performance, providing a more accurate picture of each student's capabilities than fixed-format assessments.
In the SBAC Math Test, a claim is a broad area of math skills that students are expected to demonstrate. There are four main claims for math:
- Concepts and Procedures – Using math facts and methods accurately.
- Problem Solving – Solving real-world and mathematical problems.
- Communicating Reasoning – Explaining and justifying your math thinking.
- Modeling and Data Analysis – Using math to represent and analyze real situations.
In simple terms, a claim tells what type of math skill the question is checking.
Support Every Child’s Success
Up to 3 kids. One price. Unlimited learning.
SBAC Math Test Structure: What Parents Need to Know
Computer Adaptive Test (CAT)
The SBAC Math Test is taken on a computer, and it adapts to you. If you answer questions correctly, the next ones will be harder. If you get questions wrong, they’ll get a little easier. This helps show what you really know and can do in math.
Performance Tasks (PTs)
In addition to the regular test, there’s a special part called the Performance Task. In this section, you solve a real-life math problem step by step. These problems test how well you can:
- Use what you’ve learned in math
- Think deeply and explain your ideas
- Solve problems in more than one way
For grades 3–5, a performance task usually has 4–6 questions. Some are checked by the computer, and some are scored by teachers. This format is also reflected in the SBAC ELA Test.
SBAC Math Practice Test Questions-5th Grade
SBAC Math Practice Test - Sample Question 1
Mr. Jones has 6 loaves of bread. He cuts each loaf into 4 equal pieces. How many pieces of bread will Mr. Jones have? If he sells 2/3 of these pieces, how many pieces will he sell?
Learning Tip:(SBAC Standard: 5.NF.B.4)
When working with fractions of a quantity, think of the fraction as giving you instructions! The numerator (top number) tells you to multiply, and the denominator (bottom number) tells you to divide. For example, with 2/3 of 24: First multiply by 2 (24 × 2 = 48), then divide by 3 (48 ÷ 3 = 16).
This skill will help you in everyday life, like when sharing things fairly, following recipes, or understanding sale prices. Try creating your own word problems at home using fractions of groups of objects!
SBAC Math Practice Test- Sample Question 2
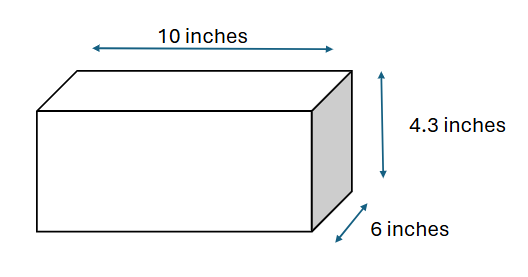
What is the volume of a rectangular prism with a length of 10 inches, a width of 6 inches, and a height of 4.3 inches?
Learning Tip:(Standard: 5.MD.C.5)
Volume helps us understand how much space an object takes up or how much it can hold. When you calculate volume, you're actually counting how many unit cubes would fit inside!
A helpful strategy is to visualize layers: First find the area of the base (length × width), then think about stacking that many cubes in layers to the height. This connects area (2D) to volume (3D).
Next time you're drinking from a juice box or unwrapping a gift, think about its volume! How many small sugar cubes would fit inside? This kind of thinking will prepare you for more advanced math in science, engineering, and everyday problem-solving.
SBAC Math Practice Test- Sample Question 3
With what number must 4.8932 be multiplied to obtain the number 48,932?
Learning Tip:(SBAC Standard: 5.NBT.A.2 )
When multiplying decimals by powers of 10, each zero in the power of 10 moves the decimal point one place to the right. This is because our number system is based on place value, where each position is worth 10 times more than the position to its right.
A helpful way to check your work is to do the opposite operation (division). If 4.8932 × 10,000 = 48,932, then 48,932 ÷ 10,000 should equal 4.8932.
Understanding how decimals move with multiplication and division will help you with money calculations, measurement conversions, and scientific notation later in your studies!
SBAC Math Practice Test- Sample Question 4
A box contains 44 books. 3/4 of the books are fiction. Of those, 2/3 are novels. How many novels are in the box?
Learning Tip:(SBAC Standard: 5.NF.B.6)
Multi-step problems with fractions are like following a trail of clues! Draw a picture or diagram to help you see what's happening.
For problems like this, try using a tape diagram or bar model:
Draw a rectangle representing all 44 books
Divide it into 4 equal parts and shade 3 parts (for the fiction books)
Take just the shaded portion and divide it into 3 equal parts, then shade 2 parts (for the novels)
This visual approach helps you see the relationships between amounts. You'll use this skill when analyzing data, calculating discounts, sharing items, and solving many real-world problems where quantities are related to each other.
Practice makes perfect—and we make practice easy.
Check out these free SBAC-style ELA sample questions for Grades 3–8 practice from other popular assessments:
SBAC Math Practice Test- Sample Question 5
Danny calculated 1.2 × 0.3 = 0.36. What mistake did Danny make?
Learning Tip:(SBAC Standard: 5.NBT.B.7)
When multiplying decimals, remember this simple rule: "Add the decimal places." Count how many decimal places appear in each number you're multiplying, then place the decimal point that many places from the right in your answer.
Here's a memory trick: If you're multiplying money amounts (like $1.25 × 3), think about whether your answer makes sense. Would three $1.25 items cost $3.75 or $37.50? The reasonable answer helps you check your decimal placement.
This decimal multiplication skill will help you calculate tips at restaurants, figure out sales tax, determine how much fabric or ingredients you need for projects, and solve countless other everyday math situations!
SBAC Math Practice Test- Sample Question 6
A rectangular garden has a length of 8 1/2 feet and a width of 3 3/4 feet. What is the area in square feet?
Learning Tip:(SBAC Standard: 5.NF.B.4)
When finding areas with mixed numbers, converting to improper fractions first makes the multiplication much cleaner! This technique works because improper fractions let you work with just one fraction instead of juggling whole numbers and fractions separately.
To visualize area with fractions, think of the garden as being divided into sections. The length (8 1/2) means you have 8 whole sections plus half a section. The width (3 3/4) means each of those length sections is divided into 3 whole parts plus 3/4 of a part.
This area calculation skill will help you in many real-life situations—planning gardens, measuring carpet or flooring, calculating paint needed for walls, and designing spaces. It's also the foundation for more advanced geometry in middle school and beyond!
Unlock every child's potential with one simple membership! Get personalized accounts, hundreds of practice tests, and individual progress tracking for up to THREE children - all at one family-friendly price. Why juggle multiple subscriptions when one can support all your children's academic journeys? JOIN TODAY and watch everyone succeed together!
Calculator and Non-Calculator Sections
Calculator availability varies by grade level on the SBAC math assessment:
- Grades 3-5: Students are not permitted to use calculators for any session of the test.
- Grade 6: Students have access to an embedded online four-function calculator during designated Calculator Available sections.
- Grades 7-8: Students have access to an embedded online scientific calculator during designated Calculator Available sections.
- High School: Students have access to embedded online calculators with scientific, regression, and graphing capabilities during designated Calculator Available sections.
External calculators are not allowed on the test, so students should practice using the approved embedded calculators before test day.
Time Allocations by Grade Level
|
Grade Level |
CAT Questions |
PT Questions |
Total Questions |
CAT Time |
PT Time |
Total Time |
|
Grades 3–5 |
31–34 |
4–6 |
35–40 |
90 min |
60 min |
150 min (2h 30m) |
|
Grades 6–8 |
30–34 |
4–6 |
34–40 |
120 min |
60 min |
180 min (3h) |
|
Grade 11 |
30–34 |
4–6 |
34–40 |
120 min |
90 min |
210 min (3h 30m) |
SBAC Scoring System and Achievement Levels
The SBAC assessments provide scores across three claim areas (Concepts and Procedures, Problem Solving/Modeling and Data Analysis, and Communicating Reasoning). Student performance is evaluated based on achievement levels that indicate their progress toward college and career readiness standards. These scores help educators and parents understand a student's strengths and areas for improvement in mathematics.
Grade-Level SBAC Math Skills: What's Tested When
Math Question Types
The SBAC math assessment utilizes a variety of question formats to measure different aspects of mathematical understanding:
Students select one correct answer from several options. These questions often assess conceptual understanding and procedural fluency
Students must select all correct answers from given options. These questions require deeper analysis and evaluation of multiple mathematical statements
Students match items in a table format, often connecting mathematical concepts, properties, or representations
Students use drag-and-drop functionality to place objects in the correct positions, such as plotting points on a coordinate plane or organizing shapes by their properties
Students enter numerical answers or mathematical expressions directly into provided fields
Students use digital tools to construct mathematical equations or expressions as their responses
Students plot points, draw lines, or create other graphical representations on a coordinate plane
Multi-step problems that require students to apply knowledge and skills to solve complex, real-world scenarios. These tasks typically include multiple related questions and may require students to explain their reasoning
Unlock Full SBAC Math Prep with Family Membership
Proven SBAC Math Practice Test Strategies That Work
Math-Specific Test Preparation Strategies
- Practice regularly with a variety of problem types to build familiarity with the different question formats on the SBAC Math Test
- Focus on conceptual understanding rather than just memorizing procedures. The SBAC Math Assessment emphasizes understanding "why" mathematical procedures work.
- Develop strong problem-solving skills by working through complex, multi-step problems that require application of multiple concepts
- Practice explaining mathematical reasoning in writing, as some questions require students to justify their solutions
How to Approach Different Question Types
- For multiple-choice questions: Read carefully, eliminate obviously incorrect answers, and solve the problem completely rather than looking for shortcuts
- For technology-enhanced items: Practice with drag-and-drop, graphing, and equation editor tools before test day to ensure comfort with these interfaces
- For performance tasks: Read the entire task before beginning, plan your approach, organize your work logically, and check that you've answered all parts of the question
Time Management for Math Sections
- Allocate time based on point values - spend more time on higher-point questions.
- Don't get stuck on difficult problems - mark them for review and come back if time permits
- Pace yourself throughout the test to ensure you have sufficient time for all questions
Frequently Asked Questions About SBAC Math Testing
Calculator allowance depends on grade level. Students in grades 3-5 are not permitted to use calculators for any portion of the test. Students in grades 6-11 have access to embedded calculators during specified Calculator Available sections only
The estimated testing time varies by grade level. For grades 3-5, the Math CAT portion is about 40-60 minutes, and the Math PT is about 60 minutes. For grades 6-11, the Math CAT portion is about 60 minutes, and the Math PT is about 60 minutes. However, the tests are not timed, so students can take the time they need to complete them
The SBAC math test includes multiple question types: multiple-choice, multiple-select, matching tables, drag-and-drop, fill-in-the-blank, equation/expression editor, graphing items, and performance tasks
SBAC math tests are scored using a combination of machine scoring and hand scoring. Multiple-choice and technology-enhanced items are typically machine-scored, while constructed-response items and performance tasks may be hand-scored. Students receive an overall mathematics score as well as scores for specific claim areas.
The SBAC math assessment is administered to students in grades 3-8 and once in high school (typically grade 10 or 11), depending on the state
Yes, the SBAC provides a range of accessibility resources, designated supports, and accommodations for students with disabilities or special needs. These are detailed in the Smarter Balanced Assessment Consortium: Usability, Accessibility, and Accommodations Guidelines



